Derivation of the Neutron Reaction Correction Equation

Addendum: Derivation of the Neutron Reaction Correction Equation^†

Jon Fleming has added this section in 2005. The purpose is to show the derivation of Cook’s “correction” equation and how non-equal cross-sections affect the result. It is based on two major premises, both of which are almost certainly false:

There is no primordial lead in the samples under consideration; all lead was created by radioactive decay and/or neutron capture.
The neutron flux was sufficient to create all the ²⁰⁸Pb in the samples, since the ²⁰⁸Pb could not have come from the decay of ²³²Th (which would leave at least a little residual ²³²Th in the samples today).

Recall the neutron-capture reaction series presented in the main text:

We’ll move from simple to more complex; starting with the end of the chain, then considering the beginning of the chain, and finally looking at the middle of the chain.

Since we “know” that all the ²⁰⁸Pb was generated by neutron capture, using C_207→208 to indicate the cross section for converting ²⁰⁷Pb to ²⁰⁸Pb by neutron capture, using N to denote the neutron flux and using ²⁰⁸Pb_measured to denote the measured amount of ²⁰⁸Pb in the sample today:

(1)

Or, solving for N:

(2)

Next we move to the beginning of the chain. Here there is one mechanism creating ²⁰⁶Pb (radioactive decay of ²³⁸U) and another mechanism destroying ²⁰⁶Pb (neutron capture). Therefore the measured amount of ²⁰⁶Pb today is less than the amount created from decay of ²³⁸U. Using ²⁰⁶Pb_Radiogenic as the ²⁰⁶Pb that was generated from radioactive decay and should be used in the determination of age; ²⁰⁶Pb_Measured as the ²⁰⁶Pb that was actually measured in the sample “today”; and ²⁰⁶Pb_Converted as the ²⁰⁶Pb that was generated from radioactive decay and then was converted to ²⁰⁷Pb by neutron capture:

(3)

²⁰⁶Pb_Converted is, of course, the amount of ²⁰⁶Pb measured times a conversion factor that is the product of the cross section (for converting ²⁰⁶Pb to ²⁰⁷Pb by neutron capture) and the total neutron flux. Since the ²⁰⁶Pb and ²⁰⁷Pb were in close proximity, the total neutron flux N is the same for both. Calling the cross section C_206→207:

(4)

Since N is the same for both ²⁰⁶Pb and ²⁰⁷Pb, we can substitute the right-hand side of equation (2) for the “N” term in equation (4):

(5)

Now we consider the middle of the neutron capture series, the amount of ²⁰⁷Pb generated from radioactive decay, ²⁰⁷Pb_Radiogenic, which should be used in the calculation of age. Here two mechanisms are creating ²⁰⁷Pb (radioactive decay of ²³⁵U and neutron capture of ²⁰⁶Pb) and one mechanism is destroying ²⁰⁷Pb (neutron capture creating ²⁰⁸Pb).

²⁰⁷Pb_Radiogenic is the measured amount ²⁰⁷Pb_Measured plus the amount of ²⁰⁷Pb that was generated by radioactive decay but then was converted to ²⁰⁸Pb by neutron capture (which in turn is equal to the amount of ²⁰⁸Pb_Measured since we “know” that all the ²⁰⁸Pb came from a one-to-one conversion of ²⁰⁷Pb) and then minus the amount of ²⁰⁷Pb that was generated from ²⁰⁶Pb by neutron capture rather than radioactive decay (which in turn is the second term of the right-hand side of equation (5)):

(6)

And, finally, dividing equation (5) by equation (6):

(7)

which, when C_207→208 = C_206→207 (as Cook assumed), reduces to the equation given in the main text except for the way that the Pb terms are grouped in the last term of both the numerator and denominator:

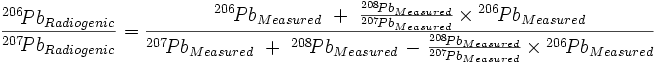
(8)

For calculating the ²⁰⁶Pb/²⁰⁷Pb for the third row of Table 5, using Dalrymple’s values for cross sections plugged into equation (7):

I do not know why my result is slightly (0.5%) different from Dalrymple’s 16.38, but the difference is not significant.

Using more recent values for the cross sections:

which is insignificantly different from the other values.

To calculate the age from these “corrected” values of ²⁰⁶Pb/²⁰⁷Pb , we use the standard equation (which cannot be solved in closed form) for age “t” of a sample (in years) given its ²⁰⁶Pb/²⁰⁷Pb ratio, the decay constant of ²³⁸U (λ₁ = 1.55125×10^-10 per year), and the decay constant of ²³⁵U (λ₂ = 9.8485×10^-10 per year) is:

(from Dalrymple, G. Brent, “The Age Of the Earth”, Stanford University Press, 1991, page 101. The values of λ₁ and λ₂ are from the same source, page 80. Note that the equation uses ²⁰⁷Pb/²⁰⁶Pb, the inverse of the lead ratios used in this paper and addendum)

The age equation is easily solved by any of a variety of numerical techniques. For ²⁰⁶Pb/²⁰⁷Pb = 16.46 the calculated age is 630 million years, and for ²⁰⁶Pb/²⁰⁷Pb = 16.47 the calculated age is 629 million years. Including the effect of non-equal cross-sections for the neutron capture reactions completely obviates Cook’s conclusion. Neutron capture does not noticeably affect the measurement of ages by ²⁰⁶Pb/²⁰⁷Pb ratios.

Introduction

I am indebted to Dr. Jamie Gilmour (Senior Lecturer, Isotope Geochemistry and Cosmochemistry, University of Manchester School of Earth, Atmospheric and Environmental Sciences) for pointing me in the right direction to understand this derivation.

Home Page | Browse | Search | Feedback | Links

How Old is the Earth

A Response to “Scientific” Creationism

Addendum: Derivation of the Neutron Reaction Correction Equation^†

How Old is the Earth

A Response to “Scientific” Creationism

Addendum: Derivation of the Neutron Reaction Correction Equation†

Addendum: Derivation of the Neutron Reaction Correction Equation^†