Other Links:
|
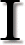 t is often asserted by creationists that the evolution of life
is impossible because this would require an increase in order, whereas the second law of thermodynamics states that "in any natural process the amount of disorder increases", or some similar claim. "Entropy" is frequently used as a synonym for "disorder".
t is often asserted by creationists that the evolution of life
is impossible because this would require an increase in order, whereas the second law of thermodynamics states that "in any natural process the amount of disorder increases", or some similar claim. "Entropy" is frequently used as a synonym for "disorder".
Of course, this represents a serious misunderstanding of what thermodynamics actually states. It can be explained patiently (or less than patiently, after the 1000th iteration or so) that entropy only strictly increases in an isolated system; that there are no completely isolated systems in nature, save maybe the universe as a whole; and that the whole idea of isolated systems is really an abstraction for pedagogical purposes; but still the creationist won't let go. There just has to be some reason why "order cannot come from disorder", and the reason must be in thermodynamics. That's the science that talks about order and disorder, isn't it?
In fact, it isn't. Look through any thermodynamics text. You will find discussions about ideal gases, heat engines, changes of state, equilibrium, chemical reactions, and the energy density and pressure of radiation. Entropy and the second law are powerful tools that allow one to calculate the properties of systems at equilibrium. At the very most, there may be a paragraph or two somewhere in that thick book alluding to some kind of relation between entropy and "disorder". Writers of pop science books like to make the same kind of relation, and will ask their readers to consider things like the state of their rooms--tidy or messy--and compare the (supposed) decrease in orderliness of the room over time to the "tendency of entropy to increase". But what of entropy and disorder? Where does that identification fit into the structure of thermodynamics?
The answer is, nowhere. It is not an axiom or first principle, it is not derived from any other basic principles, and nowhere is it required or even used at all to do any of the science to which thermodynamics applies. It is simply irrelevant and out of place except as an interesting aside. The only reason that that identification has been made stems from the different field of study called "statistical mechanics". Statistical mechanics explains thermodynamics, which is a science based on observed phenomena of macroscopic entities, such as a cylinder full of gas, in terms of more basic physics of microscopic entities, such as the collection of molecules that comprises the gas. This was a great achievement of nineteenth-century physics, led by Ludwig Boltzmann, who wrote down the only equation that connects entropy with any concept that might be called "disorder". In fact, what is commonly called "disorder" in Boltzmann's entropy equation has a meaning quite different from what creationists--and some writers of pop science--mean by disorder.
The equation in question reads:
S = k ln W.
That admittedly won't tell the reader much without some background. Boltzmann's entropy equation talks about a specific kind of system--an isolated system with a specified constant total energy E (although the constant E does not explicitly appear in the equation, it is implied and crucial) in a state of equilibrium. It tells us how to calculate the entropy, S, of that system in terms of the microscopic particles (molecules) which make it up. On the right hand side, k is a universal constant now known as Boltzmann's constant [1.38 × 10-23 joules/kelvin, for the curious --Ed]. The function "ln" is the natural logarithm, and the argument of the logarithm function is the quantity W. W is a pure number that connects the microscopic with the macroscopic.
Suppose the system we are looking at is a volume of gas inside an insulated container. The gas is specified to have total energy E, which is constant because the container is insulated so that no heat can enter or leave and rigid so that no work can be done on the gas by compression. There are roughly 1022 molecules of gas in a wine-bottle-sized container if the gas is at atmospheric pressure and room temperature. At any particular moment, each molecule is at a particular position inside the container and has a particular velocity. The position and velocity of a particle constitute its state, for Boltzmann's and our purposes. The collection of the states of all the molecules at any moment is called a microstate of the whole volume of gas. A microstate of the gas system is constrained by two requirements: first, the positions of the molecules are constrained to lie within the container (which has volume V); and second, each molecule's velocity determines its energy, and the sum of the energies of all the molecules must equal E, the total energy of the gas. An interesting question is, how many different microstates are there that satisfy these requirements at energy E and volume V? The answer to that question, provided we can calculate it, is the number W, which is the number sometimes referred to as the measure of "disorder".
Right away it can be seen that there are some problems squaring this with the everyday concept of "disorder". For one thing, this number is not even a property of any single completely specified state (microstate) of the system, but only a property of all possible microstates--in fact, it is the number of possible microstates. And W is a very large number indeed. Consider the bottle of gas: moving any one of the 1022 different molecules in it slightly from a given position counts as another microstate. Imagine then moving them two at a time in all possible combinations, then three, then four...
(As an aside, it turns out that the number of microstates, though enormous, is not infinite, as it might seem from considering that space is [so far as we know] continuous, so that one could consider moving a molecule [or adding to its velocity] by ever smaller amounts, racking up microstates with no limit. The uncertainty principle of quantum mechanics puts a lower limit on the difference in position or velocity that can be distinguished as a separate state.)
The point of thinking about the number of possible microstates consistent with the observable macroscopic state is that the system never stays in one microstate for long. In a gas in equilibrium, the molecules collide with each other constantly; with each collision their velocities change and the state changes. This happens something like 1014 times per second for every molecule in a gas at normal pressure and temperature. The states are so randomized by all these collisions that that at any given moment, every single microstate is equally probable. This is a postulate of statistical mechanics for an isolated system at equilibrium. The collection of microstates is called a statistical ensemble; it is the universe of possible states from which the system draws its actual state from moment to moment.
So in what sense can a system with large W be said to be highly disordered? Just this: the larger W is (the more possible microstates there are), the greater is the uncertainty in what specific microstate will be observed when we (conceptually) measure at a predetermined moment.
It can be seen from this that a liquid has less entropy than an equal mass of gas, and a solid has less still. In a solid, the molecules are constrained to stay very near their original positions by intermolecular forces (that is, they cannot move very far without acquiring a large amount of potential energy and thus violating the requirement that the total energy be constant and equal to E), and have average velocities much smaller than the velocities of gas molecules; but they do vibrate around their average positions and so contribute some uncertainty in the instantaneous microstate. If the solid is heated up, the vibrations increase both in size and velocity and the entropy of the solid also increases, all in agreement with thermodynamics. In fact, the statistical definition of entropy reproduces all the results of thermodynamics.
Does it make any sense to apply this to the arrangement of furniture and other items in a room in the classic pop science analogy? To do so, we would have to be sure that the situation fits all the postulates of statistical mechanics that are applicable to the statistical definition of entropy. The room could be assumed to be at least approximately isolated, if the building was very heavily insulated with no windows. We might think the room was approximately at equilibrium, if it was left undisturbed for a long time. But something is wrong here. There are an abundance of possible "microstates" of the system--as many as there are possible ways of arranging all the items in the room, and moving any item by less than a hair's breadth counts as a rearrangement. In principle, a rearrangement could be made without altering the total energy E of the system, unlike in a solid object.
But in fact, there is very little uncertainty in the actual arrangement from moment to moment. The system stays in a set of very few "microstates" for as long as we can watch without becoming bored. What's wrong? The room is not truly in equilibrium in the statistical sense--the "microstates" are not equally probable, because they are not being randomized between "measurements". The statistical definition of entropy fails, and it makes no sense to talk about the thermodynamic "disorder" of the room.
Creationists sometimes point to the complicated molecules in living cells as examples of highly "thermodynamically ordered" systems that need some special explanation, or that can only "degrade" from that highly "ordered" state because of the second law, etc. But the identification of a specified molecule with a well-defined state of thermodynamic "order" fails for a similar reason that the example of the untidy room failed.
The argument goes something like this: "There is only one possible arrangement of amino acids that makes up a specified 'functional' protein (or only one possible arrangement of nucleotides that makes up a specified gene in DNA), while there are an astronomical number of possible arrangements that are 'nonsensical' with respect to the life functions of the cell." Therefore, the functional protein (or gene) is presumably in an extremely low-entropy state, as calculated according to S = k ln W.
Is this true? This line of argument considers the overall macroscopic state of the system to be not a particular protein or a particular gene, but just "a protein" or "a gene", and considers the statistical ensemble to be the whole group of possible configurations of the same set of smaller constituent molecules. In other words, the actual "specified" macromolecule that is observed is not taken as the overall state, but only as one of the microstates.
But this runs into the same problem as the untidy room did: the configurations of molecules in cells are not randomized moment to moment; the supposed microstates are not equally probable, because once in one configuration, a molecule tends to stay in that same one. In this case, it's because there is generally an energy "bump" that has to be gotten over in the process of converting from one configuration to another. At a fixed energy less than the peak of the "bump", a pre-existing configuration will stay the way it is. If the molecule is in the same supposed microstate every time we look at it, its state is not being randomized, and it makes no sense to apply to it a statistical calculation that assumes that the probability of observing that particular "microstate" at any time is vanishingly small, when in fact, that probability is near one.
By the same token, if this line of reasoning were correct, one could look in one of the reference books where the thermodynamic properties of various chemical compounds are tabulated, and find that nearly all of them would have zero or very small specific entropies, because "there is only one way" to combine two hydrogens and an oxygen to form a water molecule, for instance. Of course, this is not the case. So how do we calculate the entropy of a molecule statistically? We calculate the number of ways it can vary--these could involve vibrational states, changes in overall shape, bond angle bending, and similar effects. These changes all leave the molecule recognizable as the same specific combination of atoms. By this calculation--the only one that matters--all the possible configurations have very similar entropies. There is no thermodynamic reason why a molecule or gene cannot, by slight changes, go from one configuration to a different one that turns out to work better.
It is worth mentioning that a statistical ensemble can also be defined for the case where the condition of constant energy is relaxed, so that energy can be exchanged with the system's environment, and another case still where both energy and matter can be exchanged. These ensembles are useful in many more practical calculations than the fixed-energy ensemble is, because only rarely do we study systems that are so well isolated that the latter can apply. Much more often the system under study is in thermal equilibrium with its surroundings, where everything has some fairly constant temperature and energy is exchanged to keep that temperature equal on both sides of the system boundary. When this is the case, the most important change is that the microstates of the ensemble are not all equally probable, and instead of Boltzmann's equation we have to use for the entropy the more generalized equation,
S = -k Σ Pi ln Pi
Here Pi is the probability of the ith microstate, and the Greek capital "sigma" (Σ) means that we take the sum over all the microstates. This formula was first written by another of the founders of statistical mechanics, the American physicist J. W. Gibbs. This is a more complicated expression, but has the same basic meaning as Boltzmann's formula: the entropy is a measure of the uncertainty in which microstate will be observed in the next measurement. By using the mathematical properties of probabilities and of the logarithm function, it is simple to show that if the probabilities are in fact all equal, Gibbs' formula reduces back to Boltzmann's original equation, as it should.
Here's a quick quiz. Which of the following patterns is more "ordered" in the thermodynamic sense?
ABAABBABBBBBABBAABABB
ABAABAABAABAABAABAABA
AAAAAAAAAAAAAAAAAAAAA
ABABABABABABABABABABA
Answer: the question is meaningless, because none of the patterns is an ensemble; all are possible individual microstates of some unspecified ensemble. Statistical mechanics, and by extension thermodynamics, has exactly nothing to say about the kind of order we think about intuitively in everyday life.
[Back to the Thermodynamics FAQs]

Home Page |
Browse |
Search |
Feedback |
Links
The FAQ |
Must-Read Files |
Index |
Creationism |
Evolution |
Age of the Earth |
Flood Geology |
Catastrophism |
Debates