
Debunking Robert Gentry's
"New Redshift Interpretation" Cosmology
by Ryan
Scranton
[Links updated: July 24, 2003]
![]()

![]()
Other Links:
|
![]() he purpose of this FAQ is not to describe in
full or even in part the standard Big Bang cosmology that
young-earth creationist R.V. Gentry means to replace with
his New Redshift Interpretation
(NRI). The description of
the standard cosmological model and answers to common
questions have already been very capably elucidated by
Professor Ned Wright in his Cosmology
FAQ ; further information about standard cosmology can
be found in the texts referenced at the end of the FAQ.
Rather, this FAQ is intended to address the problems in Dr.
Gentry's NRI which might not be obvious to someone
unfamiliar with the areas of physics involved. Dr. Gentry
has also submitted preprint which argues against the
standard cosmology and for the NRI which will be dealt with
in a separate section from the rest of the Dr. Gentry's
model.
he purpose of this FAQ is not to describe in
full or even in part the standard Big Bang cosmology that
young-earth creationist R.V. Gentry means to replace with
his New Redshift Interpretation
(NRI). The description of
the standard cosmological model and answers to common
questions have already been very capably elucidated by
Professor Ned Wright in his Cosmology
FAQ ; further information about standard cosmology can
be found in the texts referenced at the end of the FAQ.
Rather, this FAQ is intended to address the problems in Dr.
Gentry's NRI which might not be obvious to someone
unfamiliar with the areas of physics involved. Dr. Gentry
has also submitted preprint which argues against the
standard cosmology and for the NRI which will be dealt with
in a separate section from the rest of the Dr. Gentry's
model.
The material from this FAQ was compiled by Ryan Scranton from postings on talk.origins from Sverker Johansson, Steve Carlip, Ken Cox, Mark Kluge, and Ryan Scranton. Any and all comments can be sent to scranton@oddjob.uchicago.edu
The material in this FAQ, both that which supports in the NRI and that which refutes it, is very technically involved. For the casual reader, it may be very difficult, when confronted with two opposing arguments about an unfamiliar and complicated subject, to determine who is right, who is wrong or if both sides are merely making jargon-filled arguments which are meaningless. The only real solution to this problem is to educate oneself about the material involved so as to make an informed decision. However, since most people reading this don't have time to take the 3 or 4 years of physics classes that would be needed to get a handle on the depth of the arguments, this section hopes to provide a short outline of the rest of the FAQ, as well as answers to a few questions that might spring to mind when trying to judge the validity of the arguments presented therein.
The NRI consists of three main components:
The problems with this model are (at least) five-fold:
| 1. General relativity | Dr. Gentry claims that his model is "based on a universe governed by static space-time general relativity. But in fact, the model is inconsistent with the Einstein field equations, the basic equations of general relativity. |
| 2. "Fine tuning" | The NRI can reproduce observed
features of the universe only by adjusting parameters in
the model by hand. For example, it gets the right
temperature of the cosmic microwave background radiation
only because the temperature can be set to any value Dr.
Gentry wants in his model.
More dramatically, he gets the "Hubble relationship"---the fact that galaxies recede from us at a speed proportional to their distance---only by choosing initial conditions in which this relation is built in. In other words, Dr. Gentry's model must separately adjust the velocity of each galaxy in the universe at some initial starting time to be just right. |
| 3. Stability and consistency | In Dr. Gentry's model, galaxies are
all moving away from us. Yet he also assumes that the
density of galaxies doesn't change with time, i.e., that
the universe doesn't "thin out." This is only possible if
new matter is somehow continuously created (as in the old
"steady state model") to replace the objects that are
moving away.
Dr. Gentry's universe is surrounded by a shell of hot hydrogen that is supposed to provide the observed cosmic microwave background radiation. But this shell is heavy enough that it should collapse inward under its own weight, in a time too short to give the proper background radiation. To provide the right spectrum of cosmic microwave background radiation (a black body spectrum), Dr. Gentry's hydrogen shell has to be thick and dense enough to be "opaque." If you put in the numbers required by the model, the shell comes out much too thin, nearly transparent, and can't give the observed spectrum. Dr. Gentry demands that his hydrogen shell that surrounds the observed universe be surrounded in turn by empty space. In such a configuration, the shell will cool to near absolute zero very rapidly; it won't stay hot nearly long enough to give the observed background radiation. |
| 4. Observations | One of the key observations Dr.
Gentry's model tries to explain is the red shift-distance
relation, that light from distant galaxies is shifted to
the red end of the spectrum in an amount proportional to
their distance. The model gives the right result for
relatively nearby objects, but deviates from the observed
relationship for more distant objects, giving a prediction
that is clearly ruled out by recent observations of distant
quasars.
We observe that the number of quasars falls of rapidly at large distances. Dr. Gentry's model has a mechanism to explain this, but it sets in at distances that are much too small, giving a badly wrong prediction for the distribution of quasars. Gentry's model gives a prediction for the surface brightness of galaxies as a function of distance that seems to disagree with recent observations. (These observations are still difficult enough to do well that this problem is probably not fatal.) |
| 5. Missing observations | The standard big bang model
successfully explains the observed abundances of light
elements, which are created by nuclear reactions in the
very hot early stages of the universe. Gentry's model must
dismiss this success as coincidence, and offers no
alternative source for these elements.
In the standard big bang model, the age of the universe sets a natural scale for the age of old objects (the oldest stars, for instance). While details remain uncertain, the ages generally agree. In Gentry's model, this must again be dismissed as mere coincidence. |
| Q: If the flaws in the NRI are as obvious as the FAQ writers would have one believe, why didn't Dr. Gentry see them? | A: The most cynical response would be that Dr. Gentry ignored the problems with the model in order to provide more grist for creationists to use in their efforts to hinder "dangerous" science like cosmology and evolution. The more likely case is that Dr. Gentry was doing work outside of his area of specialty (geophysics) and thus he was less likely to notice problems which would be readily apparent to someone familiar with the requirements that physics puts on astronomical and cosmological models. Likewise, he may not have been as conversant with the observational evidence that would support standard cosmology to the detriment of his model. |
| Q: So how did this get by the reviewer if someone familiar with the field would have spotted these errors? | A: The simple answer is that the peer-review
process is not perfect; if all of the papers that made it
through the process were completely free of faults and
completely consistant with all of the known evidence, the
journals would be very thin indeed. The referees for the
papers, while very knowledgable are not omniscient.
However, limitations of the review process are well known
within the scientific community, and, as such, the
submission of an idea is only the first step in its
acceptance by the community at large. Once an idea has been
published, it is up to others to verify or refute the
claims made in the paper (likewise, the original authors).
After succeeding in this process for several iterations, an
idea gains some measure of acceptance.
For the NRI, we are at the second stage of that review, where the claims are put before the scientific community, and, as outlined above and detailed below, are found wanting. |
Dr. Gentry's NRI model was first presented in Modern Physics Letters A. The standards that different journals have for articles and letters (which should not be confused with letters-to-the-editor style documents) vary considerably. MPLA, in particular, tends to publish shorter papers that might not have been appropriate for the generally more prestigious Physical Review, but they do subject their papers to peer-review before publication. This is in contrast to the preprint that Dr. Gentry submitted to the Los Alamos National Laboratory archive; the only qualification for acceptance of a preprint is some manner of association with an established institution. While the FAQ will briefly outline Dr. Gentry's model, readers are encouraged to examine for themselves his MPLA letter and his LANL preprint.
In the standard cosmological model the large-scale matter distribution of the universe is assumed to be isotropic and homogeneous. As Dr. Gentry indicates, the former assumption has been well established by observations of the angular distribution of galaxies in galaxy surveys. On the other hand, the assumption of homogeneity is difficult to directly verify due to the fact that we cannot (now or in anything resembling the near future) observe the universe from any different vantage point than our own galaxy (It should be noted, however, that while the homogeneity of the distribution matter cannot be determined directly, it can be supported indirectly by verification of predictions made by assuming it. For instance, the prediction and observation that the cosmic microwave background radiation would be isotropic to a very high degree is made in standard cosmology using the assumption of homogeneity). The NRI eliminates the assumption of homogeneity and posits a universe with a definite center, near which the assumption of isotropy is valid. Additionally, while the standard cosmology includes an expanding universe in which the distance between two coordinates in space-time increases over time, the NRI claims to be a static universe.
The matter in the NRI universe is distributed uniformly in a sphere around the center of the universe with radius 4.365 Gpc (1 Gpc =109 parsec, 1 parsec = 3.26 light years). Surrounding this sphere is a thin shell of hot hydrogen. Beyond the hydrogen shell, the matter density is assumed to fall off expontially in the radial direction. Additionally, the NRI makes use of a non-zero vacuum energy density. This energy has negative mass and acts as a repulsive force, rather than gravity's normal attractive nature. This concept (the "cosmological constant") was first introduced by Albert Einstein in order to keep the solutions to his General Relativity Field Equations static rather than resulting in a universe which eventually collapsed into a singularity (Upon hearing of Hubble's observations of the isotropic motion of distant galaxies away from ours, he later discouraged the inclusion of the cosmological constant in his field equations; it has recently come back in vogue to explain observations of high redshift supernovae by Perlmutter and Riess.). The final critical component of the NRI is the notion of gravitational redshifts. These redshifts are due to time dilation experienced by observers in different gravitational potentials; the effect is very small under conditions founded on the Earth, but can be very pronounced if the difference in potential is very large. This time dilation was predicted by General Relativity and has since been confirmed both on Earth and via astronomical observations.
The two cosmological observations that Dr. Gentry seeks to incorporate into model are the cosmic microwave background radiation (CMBR) and the Hubble relation. The CMBR is a diffuse isotropic bath of radiation that has the same spectrum as a black body at approximately 2.7 K to better than one part in 10,000. In the standard model, this radiation is the remnant of the point in the expansion of the universe that radiation decoupled from matter due to the recombination of electrons and nuclei into hydrogen and helium. In the NRI, this radiation is due to the hot shell of hydrogen that surrounds the observable universe. This hydrogen radiates as a black body and the radiation is redshifted due to the difference in gravitational potential between it and the center of the universe to the 2.7 K CMBR that we observe. Dr. Gentry sets the gravitational potential equal to zero at the center of the universe, which allows him to express the mass of the hydrogen shell ( Mg) as
| Mg = 2 |
(1) |
where R is the radius of the shell, v is the vacuum energy density
and
is the mean matter density of the sphere
within the shell. In his paper, Dr. Gentry assumes a
temperature for the hydrogen shell of 5400 K, resulting in
a redshift of the temperature of
| z + 1 = (1 + 2 |
(2) |
where z is the ratio of the difference between
the observed and emitted wavelength and the emitted
wavelength of the photons,
is the gravitational potential at the shell and c is
the speed of light. The precise temperature of the hydrogen
shell is not terribly important since the equation that
determines the resulting redshift goes very rapidly to
infinity near the value that Dr. Gentry cites for R
(4.365 Gpc); thus nearly any temperature could be
redshifted down to 2.7 K without changing the radius of the
shell significantly (see Fig. 1). Although not stated
explicitly, Dr. Gentry's redshift relation for the
temperature sets the time scale of the NRI such that
| HR/c = 1 | (3) |
Thus, the minimum age of the NRI model (as required for the volume inside the shell to be filled with photons from the shell) is 1/H.

|
In its simplest form, the Hubble relation states that the apparent velocity (as inferred by the observed redshift of the light from the galaxy) of a galaxy is related to the distance to the galaxy (r) by
| z = Hr/c | (4) |
where H is Hubble's Constant (current measurements of H put it at approximately 65 ± 8 km/s/Mpc). In the standard cosmology, this relationship can be derived from the field equations in the limit of small z as
| Hr/c = z + .5(1-q)z2 | (5) |
where q is known as the "deceleration parameter" and is related to the matter and vacuum energy densities of the universe. In the NRI, Dr. Gentry seeks to explain the first Hubble relation by means of gravitational repulsion. If the magnitude of the vacuum energy density is greater than half the magnitude of the matter density (the factor of one half is due to the pressure associated with the vacuum energy density and lack thereof from the matter), then the effective negative mass within a radius r will result in a positive acceleration in the radial direction of
|
d2r/dt2 = 4 |
(6) |
where d2r/dt2 is the acceleration (second derivative of r with respect to time) and G is Newton's Constant. Given certain initial conditions the above differential equation yields an expression for r which increases exponentially with time,
| r =
rgeHt, H2 = 4 |
(7) |
where rg is the initial radial position of the galaxy. Taking the derivative of this expression with respect to time yields the expression
| v = Hr | (8) |
Since the galaxies will be in motion, as well as at different potentials from our galaxy, the observed redshift relation must take both of these effects into account. After substituting his expressions for potential at a given radius and velocity, Dr. Gentry gives the redshift of a galaxy as
| z + 1 = (1 + Hr/c)/(1 - (2 + ug2 )(Hr/c)2).5 | (9) |
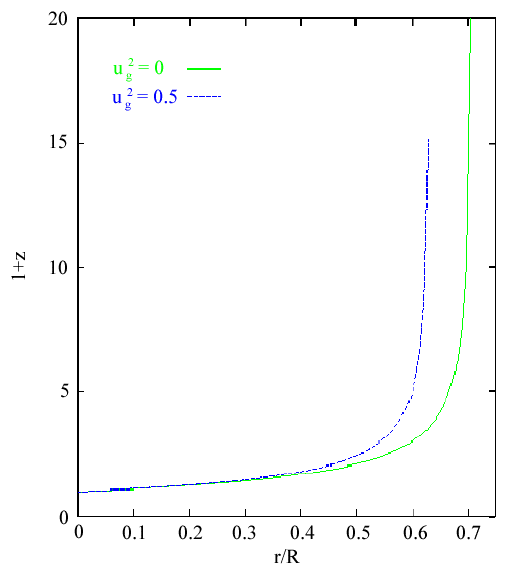
where ug is the ratio of a given galaxies tangential velocity to its radial velocity (see Fig. 2). For sufficiently small values of r this reduces to (3).
|
The difficulties with the NRI can be broken into four broad categories: general relativistic errors, Hubble relation problems, hydrogen shell problems, and missing observations.
For his model to be consistent with General Relativity, the NRI must be a valid solution to the Einstein Field Equations. The explicit metric (a system of equations governing the geometry of spacetime in his model; see below) of the NRI is not given in his paper, but the parameters that he cites (radial homogeneity, spherical symmetry, and a metric that does not change with time, or "static" metric) are enough to demonstrate an inconsistency with the only applicable solutions to the Field Equations.
In order to maintain a static universe, as Dr. Gentry claims the NRI is, the radial pressure gradient, as given by the Oppenheimer-Volkov equation
| dP/dr = (P + |
(10) |
where P is the pressure and M(r) is the mass contained within radius r, must equal zero. If this is not equal to zero, then there will be a resulting imbalance of forces which either pushes the matter away from the center of the universe (if the pressure force is too strong) or pulls the matter towards the center of the universe (if the gravitational force is too strong). For densities which do not vary with radius (as in the NRI), there are two possible static solutions: the de Sitter solution and the Einstein solution. In the de Sitter solution, the pressure is given by
| P = - |
(11) |
(there is no normal matter), making the first term of (10) equal to zero. The Einstein solution has
| P = - |
(12) |
If we substitute this into the second term of (10), we get
| 4 |
(12a) |
where we have expanded M(r) in terms of ( -
v). Thus, in order to make
this term zero (and satisfy dP/dr = 0), the Einstein
solution requires that
= 2
v.
By postulating a model in which neither of these is true, (indeed, where the Einstein solution is explicitly not true) the NRI universe has a positive pressure gradient and must therefore expand, contrary to Dr. Gentry's claims. Further, if the NRI were truly an Einstein static model, then there would be no motion due to difference in potential nor any redshift due to the same (cf. (1), (7)). The NRI could avoid this by removing the condition that the pressure and density be radially homogeneous, but this would lead to drastic disagreement with observation (Goodman, Phys. Rev. D52 (1995) 1821). Thus, in effect the model is merely a spherical slice of the standard cosmological model surrounded by a shell of hydrogen.
While the above is certainly a serious problem with the model, it is merely a symptom of the greater problem of the NRI with respect to General Relativity. Despite Dr. Gentry claims that the NRI is in accordance with General Relativity, a solid relativistic basis for the NRI is seriously lacking in this paper. His paper makes no mention of the metric for his model, without which one cannot know the equations which govern motion in his model; simply claiming to be governed by a static metric is not enough (particularly when there is ready evidence that the metric would not be static). This means that, for instance, there is no way of knowing whether Dr. Gentry's use of the Newtonian equations of motions for galaxies in his model is justified, nor can one determine on what scales his equations of motions might break down. Indeed, there is not even a mention of the fact that the expression for his "Hubble Constant" requires that the radius of the hydrogen shell also be equal to the Schwartzchild radius (This is the radius at which, for a non-rotating black hole, matter and light can no longer escape the black hole's gravitational potential and will eventually be drawn towards the singularity at the center) or how he would propose to match boundary conditions between the metric of the shell and the outside universe at this point. Rather, the use of gravitational redshifting is merely a thin veneer for what is, in description, a model which is a Newtonian universe with flat, Euclidean geometry.
In his derivation of the motion of the galaxies due to the enclosed negative mass, Dr. Gentry cites equation (5) as the equation governing the acceleration of the galaxy at radius r due to the gravitational repulsion of the negative mass contained within that radius. However, in order to arrive at the equation for the behavior of the galaxy with time, he must assume boundary conditions for the initial position (which he does explicitly) as well as the initial velocity (which he does not mention explicitly). Thus, his derivation actually requires that the galaxies have an initial velocity proportional to their initial position in order for the (6) to be true. This is not only circular reasoning, but would also require the velocity of each galaxy to be fine tuned to the appropriate velocity. In the standard model, there is no such requirement; galaxies may have any initial velocity due to their local environment (being a part of a galaxy cluster, like our galaxy is part of the Local Group, for instance), and the expansion of the metric will merely add the appropriate radial velocity without fine tuning.
Additionally, his derivation assumes that the matter density and the vacuum energy density do not change with time. While this is valid for the vacuum energy density (which is a property of spacetime and, hence, unchanging), the matter density will not remain fixed. Treating the matter as a fluid, conservation of matter requires that
| d |
(13) |
where (
v) is the divergence of
the matter density times the velocity. This is simply
another way of saying that the change in matter over time
for a given volume is going to be equal to the amount of
matter that flows in or out of the volume element. Ignoring
transverse velocities, we can expand the right side of the
equation as
| (14) |
where we assume that v = Hr. The first term is straightforward to evaluate
| (15) |
The second is not so easy. If we assume an initially
radially isotropic distribution of matter ( is independent of r), then this term
vanishes. This would mean that the time scale for the
change in matter density (
divided by the
absolute value of d
/dt) is
1/(3H), one third the Hubble time (1/H =
13.75 billion years for H = 65 km/s/Mpc). However,
since the gradient of the density is going to be positive
with increasing r as more and more the galaxies and
intergalactic material move along their exponential
expansion, the value of the second term of
(14) is going to
become greater that 0, driving the matter density depletion
time scale ever shorter. The result of all of this is that
if the Hubble time is the dynamic time scale for the NRI,
then Dr. Gentry's derivation of the Hubble relation from
his model is inaccurate.
Lastly, while the redshift relation that Dr. Gentry presents is approximately linear for small values of r, its diverges from linearity very rapidly. At z = .1, the deviation from linearity is 10%; by z = .5, it is 50%; and at z = 1, the deviation is over 100% (see Fig. 3). This is in marked contradiction to the predicted Hubble expansion in (5). More importantly, the value of of q that would be required to approximately match the NRI relationship has been excluded by observations of distant supernova (cf. Perlmutter, et al. ApJ 483:565 (1997).)

|
This non-linearity also leads to problems with one of the areas that Dr. Gentry claims as his strongest supports, quasar number counts. As shown in Fig. 2, the rapid rise in redshift at ~.7R means that an object could very rapidly have its light redshifted beyond observation with only a small change in distance from the center of the universe. Dr. Gentry takes this as explanation for the dearth of quasars beyond a redshift of z = 4. However, as Fig. 3 indicates, this effect actually sets in at a much lower redshift than Dr. Gentry would lead us to believe. Assuming that the distribution of quasars is uniform, it can be readily shown that the ratio of the predicted number of quasars in with a redshift between z and z + dz in the NRI to the standard cosmology is .39 at z = 1 and .18 at z = 2. While this is not evidence in and of itself, the fact that the NRI number density decreases from z = 0 to z = 2 is sharply contradicted by the observed increase in quasars over that same redshift interval (M. Rees, Perspectives in Modern Cosmology, Cambridge University Press, 1995)
As mentioned in the description of the derivation of (2) for the redshift of the black body emission of the hot hydrogen shell, the expression diverges to infinity for values of r near R and thus there is very little constraint on the temperature of the shell. This is particularly unsatisfying from an aesthetic standpoint, since it lends a measure of unfalsifiability to the theory; something which should be avoided in science. Thus, while we might expect emission lines from the hot hydrogen to show up in the spectrum (contrary to our observations of the CMBR), this redshift relation would allow the temperature to be low enough to prevent significant emission without changing the value of the shell's radius significantly.
More problematic, however is the question of the shell's stability, both against small and large scale collapse. Considering first the small scale, there are two requirements. First, the shell must be thin enough that the thickness of the shell not exceed the Jeans Length, Rj. If the shell were thicker than that, then it would begin to collapse radially (not towards the center of the universe, but rather the two sides of the shell towards each other) because the gravitational pull of the shell on itself would exceed the the pressure of the gas in the shell. This requires that the shell thickness be just less than
| Rj = ( |
(16) |
where k is Boltzmann's Constant, T is the
temperature, n is the number density of the hydrogen
and m is the mass of a hydrogen atom. Second, the
shell must be opaque enough that it radiate as a black body
as required for the CMBR. This means that the optical depth
() must be
| (17) |
where is the scattering cross-section
for the hydrogen. In the likely temperature regimes for the
shell, this should be the Thomson cross-section. Now that
we have an expression for the number density of the gas in
the shell as well as a thickness, we can calculate the
minimum mass that the shell would need to radiate as a
blackbody and be stable against self-gravitation. The the
mass of the shell should be
| Ms = 4 |
(18) |
where Rs = R + Rj. Using the fact that Rj » R, we can re-write (18) as
| Ms = 4 |
(19) |
Substituting for Rj and n, we get
| Ms » 4 |
(20) |
which is independent of the temperature of the shell. For R = 4.365 Gpc, Ms » 2.9 × 1024 solar masses. Using Dr. Gentry's values for H and R, the mass of his shell is about 1.3 × 10 23 solar masses, thus missing the absolute lower limit of the mass of the shell by a factor of 20. In order to attempt to make up for this deficit, one could increase the values of either H or R. However R cannot be increased sufficiently beyond the value that Dr. Gentry cites without causing the redshift of the photons coming from the shell to increase to infinity and H cannot be increased enough if he wishes to stay within the error bars of the current measurements.
On the subject of large scale stability, even if Dr. Gentry uses Mg (from (1)) for his shell, the shell is still going to have a greater absolute mass than that of the mass that it encloses. Following Dr. Gentry's treatment, the mass enclosed by the outer layer of the hydrogen in the shell is going to be
| Mg - M = 2 |
(21) |
where M is the magnitude of the mass of the
sphere enclosed by the shell. The fact that this is
positive means that pressure due to the vacuum energy
density is not going to be enough to counteract the
gravitational pull of the shell, and it will begin to
collapse towards the center of the universe. The time scale
() for this
collapse will go as
| (22) |
where d2R/dt2 is the second derivative of radius with respect to time. From Dr. Gentry's expression,
| d2R/dt2 = -GM/R2 | (23) | |
This is nearly the inverse of the expression that Dr. Gentry has for Hubble's Constant (it's actually 1/((2/3)H).5), meaning that not only is Dr. Gentry's assumption that the shell will be stationary bad, but it will be contracting on approximately the same time scale that mass inside the shell would be expanding outward due to the negative mass, assuming that the divergence of the mass density is negligible. In short, if Dr. Gentry means the Hubble time to be indicative of any sort of dynamic time scale in his model, then that will also be the time scale that everything falls apart on him.
Lastly, we can readily see that the cooling time of the shell is far too rapid to account for the steady CMBR background that is observed. Basic thermodynamics tells us that the thermal energy of a hydrogen atom in the shell at temperature T is going to be 1.5kT (where k is Boltzmann's constant and we are assuming that the hydrogen exists only as single atoms due to the very low density). If we use the requirement that the shell radiate as a black body to give us an expression for the number of hydrogen atoms in the shell, then the total thermal energy of the shell is
| E = 4 |
(24) | |
| = 6 |
||
where T is the Thomson
scattering cross-section. Assuming thermal equilibrium on
the inside of the shell, the luminosity (the amount of
energy emitted in a given amount of time) of the shell is
going to be given by the standard formula for radiation by
a black body,
| dE/dt = 4 |
(25) |
where B is the
Stephan-Boltzmann constant. Thus, the cooling time scale is
going to be
| (26) |
For T = 5400 K, Tau is about 35 seconds. In order to still be radiating after a Hubble time, the temperature would have to be on order 10 mK. Indeed, if the temperature of the hydrogen shell were the 2.7 K observed for the CMBR today (ignoring redshift effects), the cooling time would be less than 9000 years.
Not only does this tell us that the initial thermal energy of the shell will be radiated away very quickly, it also means that any extra thermal energy that the shell would pick up as it dumped gravitational energy during the collapse would be radiated away almost immediately. Additionally, if the shell were to start with a combination of number density and shell thickness that was optically thick enough to radiate as a black body, the decrease in temperature would rapidly drive down the Jeans length, making the shell instable to the small scale collapse detailed in the first part of this section.
While the NRI claims to succeed in matching the observations of two of the three major supports for the standard cosmological model (the CMBR and the Hubble Relation), it completely ignores the success of the third, Big Bang nucleosynthesis. By modeling the nuclear reactions that would have taken place in the first 3 minutes after Planck time, cosmologists (notably Alpher, Bethe and Gamow, who published the seminal paper on the subject, Phys. Rev. 70:527 (1946); and Alpher, Follin and Herman, who laid the foundation for the code to calculate the Helium-4 abundance, Phys. Rev. 92:1347 (1953)) have been able to accurately predict the relative abundances of light elements in the interstellar clouds that have persisted since the Big Bang and explain the lack of heavier elements in the oldest stars that we observe in our galaxy. In particular (but not exclusively), the predictions that the Helium-4 abundance would be approximately 25% that of Hydrogen and that the Deuterium abundance would be non-zero if the matter density of the universe in baryons were not equal to the critical density needed to close the universe have been confirmed by observation (cf. Schramm and Wagoner, Ann. Rev. Nuc. Part. Sci. 27:37 (1979); Austin, Prog. Part. Nuc. Phys. 7:1 (1981); York, et al. ApJ 276:92 (1984)). The former is important in that it was the prediction least sensitive to the variations of parameters that go into the model and the latter because Deuterium is rapidly consumed in stars due to a low binding energy and hence would not be produced in significant amounts in any other known process. A more complete description of BBN, its confirmations and its utility as a probe of cosmological parameters can be found in Principles of Physical Cosmology by P.J.E Peebles (Princeton University Press, 1993) and The Early Universe by Kolb and Turner (Addison-Wesley Publishing, 1990), both of which are also excellent texts on cosmology in general (although one should be fore-warned that they are not intended for a lay audience). Other review articles of interest are
In Dr. Gentry's NRI model the light element abundances and the similar time scales for the oldest stars and the age of the universe is merely a coincidence. It is completely silent on both of these points, to its detriment.
Dr. Gentry's "Rosetta" preprint consists of essentially two parts. In the first, Dr. Gentry contends that the expansion of the universe in the standard cosmology and attendant redshifting of photons traveling in that expanding metric results in a violation of the conservation of energy in the universe and he presents an estimate of the energy "lost" during the tenure of the universe. Secondly, he refers to a number of experiments which lend credence to the predictions from general relativity concerning redshifting of light due to gravitational potentials. As a conclusion, he notes that recent supernovae observations lend credence to his inclusion of a non-zero vacuum energy density in the NRI and that, as he feels that the problems with the standard cosmology he outlines do not exist in his NRI, it should be the preferred model.
In short, both of the points that Dr. Gentry describes are not exclusive to the standard cosmological model, but rather are objections which demonstrate how general relativity does not match our everyday intuition (even when that intuition might be guided by work in another area of physics). While conservation of energy is a straight-forward matter to deal with in the Newtonian limit (as presented in Dr. Gentry's calculation), when the curvature of the metric is taken into consideration, things become much more complicated. Non-gravitational energy may be easily accounted for (as Dr. Gentry's straightforward calculation shows) in a covariant tensor; however, due to Einstein's equivalence principle, there can be no such tensor for gravity.
Contrary to Dr. Gentry's claims, this is dealt with in a number of texts and addressed quite well in the Sci.Physics Relativity FAQ (which includes a sampling of the aforementioned texts). The complete answer requires careful consideration of the energy-momentum tensor and its covariant derivative (similar to a standard derivative, but with an extra term to account for the curvature of space-time) and is best discussed in the texts. One possible interpretation of the very complex mathematics involved is that the energy which is "lost" in Dr. Gentry's calculation can actually be accounted for in the curvature energy of the metric. Another intrepretation is that, while our notions of energy conservation are supported in the weak-field limit, relativity indicates that they do not hold in general (as indicated in the quote from PJE Peebles that Dr. Gentry cites in his paper). Since the NRI claims to be based upon general relativity, one may just as well ask where the energy from the 5400 K spectrum goes when we only receive the much redder and energy depleted 2.7 K spectrum in the NRI; the answer is along the same lines.
Dr. Gentry's second point is moot. As mentioned earlier in the FAQ, the evidence for redshifts due to gravitational redshifts is very good, and that they exist is not in contention here. Indeed, if they did not it would be a very serious problem for standard cosmology since it would indicate an error in the theory of general relativity, which is the core of Big Bang theory. However, by supplying evidence for the precision of these measurements, Dr. Gentry means to imply that the redshifts due to the cosmological expansion of the metric which should also be seen in these measurements is not observed.
This ignores the fact that the FLRW (Friedman, Lemaitre, Robertson and Walker) metric which describes the geometry of standard cosmology is only taken to be valid on the largest scales (on order 100s of Mpc) where the distribution of matter is smoothed out, while all of the examples that Dr. Gentry cites are for phenomena on scales at least four orders of magnitude too small. These are all regions of over-density which have fallen out of the Hubble expansion due to their own self-gravity. Thus, that space-time does not expand on these smaller scales is perfectly in line with the standard cosmology's prediction that it should not. Dr. Gentry's mention of the apparent contradiction in an expanding metric still allowing discrete emission spectra (which is not a contradiction since the emission happens on scales much smaller than those of the FLRW metric as explained above) casts serious doubt as to whether Dr. Gentry recognized this basic distinction when writing the paper.
Lastly, his claim that the recent work by Perlmutter and Riess on the supernovae surveys supports his inclusion of a vacuum energy density in his model ignores the fact that the results that these two groups obtained which find a non-zero value for the cosmological constant are only such in the context of the standard flat universe model. They can just as easily be explained by a standard open universe model. In summation, the objections to the standard model that Dr. Gentry lists in his preprint are not specific to standard cosmology, but rather are subtle features of general relativity. These issues were recognized and resolved by the scientific community early in the history of general relativity and cosmology and the reasons the arguments are invalid serve as common subject matter for introductory courses in the field.
While Dr. Gentry's model apparently escaped criticism by
whatever review went on before being published in MPLA,
upon further examination it is seriously lacking. Despite
claims to be a static solution to the Einstein Field
Equations, the NRI, in fact, is not. Even while assuming
the simple Hubble Relation as an initial condition it fails
to match the observed linearity in variation of redshift
with distance. While its elements may persist for a short
time in the configurations that Dr. Gentry describes, the
matter inside the hydrogen shell and the insufficiently
massive hydrogen shell will significantly diverge from
their initial positions in less than a Hubble time. Lastly,
the NRI completely fails to account for the observed light
element abundance. This all makes Dr. Gentry's preprint
claim to have found the "Genuine Cosmic Rosetta Stone" in
his NRI seriously questionable.

| Home Page | Browse | Search | Feedback | Links |
| The FAQ | Must-Read Files | Index | Creationism | Evolution | Age of the Earth | Flood Geology | Catastrophism | Debates |